[Jens N.]

Wie berechne ich den max. Abbildungsmaßstab (und idealerweise auch noch die resultierende Nahgrenze) eines Objektivs bei Verwendung eines Zwischenrings? Die Angaben, die ich im Netz gefunden habe, bezogen sich meist nur auf unendlich Fokussierung (z.B. 50mm ZwiRi an 50mm Objektiv = Maßstab 1:1, aber das kann ja für ein 50er Makro z.B. kaum gelten). Wenn ich das richtig verstanden habe, muß/kann man da noch den Auszug hinzurechnen, den jedes Objektiv bei Fokussierung auf die Nahgrenze von sich aus mitbringt - nur woher bekomme ich ich diesen Wert?

Der Zwischenring ist 25mm breit, Brennweiten und max. Abbildungsmaßstäbe, bzw. Nahgrenzen der in Frage kommenden Objektive sind bekannt. Einfach ausprobieren wäre zwar eine Möglichkeit, ist mir aber zu stressig.

[bleibert]

Zitat von Jens N.

Wenn ich das richtig verstanden habe, muß/kann man da noch den Auszug hinzurechnen, den jedes Objektiv bei Fokussierung auf die Nahgrenze von sich aus mitbringt

Genau, ein Zwischenring ist einfach nur eine weitere Auszugsverlängerung, genau, wie beim Fokussieren.

- nur woher bekomme ich ich diesen Wert?

Na, einfach ausrechnen!

Nehmen wir mal ein Objektiv mit f=50mm und einem Abbildungsmaßstab an der Nahgrenze von Beta=0,5 (also 1:2). Dann errechnet sich die Bildweite b wie folgt:

1/f = 1/g + 1/b

1/g = 1/f - 1/b = (b-f)/(b*f)

Beta = b/g = b*(1/g) = b*(b-f)/(b*f) = (b-f)/f

b = Beta*f + f = 0,5*50mm + 50mm = 75mm

Allerdings wissen wir ja auch, dass sich die Bildweite b aus der Brennweite f und der Auszugsverlängerung x zusammensetzt:

b = x + f = Beta*f + f

x = Beta*f

Also ist die Auszugsverlängerung immer gerade Abbildungsmaßstab mal Brennweite, bzw der Abbildungsmaßstab ist die Auszugsverlängerung geteilt durch die Brennweite:

Beta = x/f

Beta[Zw] = (Beta[Ng]*f + [Zw])/f

Somit berechnet sich der Abbildungsmaßstab mit Zwischenring Beta[Zw] aus dem Abbildungsmaßstab bei Nahgrenze Beta[Ng] mal Brennweite zzgl. dem Maß des Zwischenringes [Zw], und das ganze geteilt durch die Brennweite. Bei obigem Beispiel:

Beta[25mm] = (0,5*50mm + 25mm)/50mm = 1

Nehmen wir mal ein hypothetisches 135er mit Nahgrenze 1m und dort erreichtem Abbildungsmaßstab von ca. 1:5 = 0,2:

Beta[25mm] = (0,2*135mm + 25mm)/135mm = 0,4

Oder ein ebenso hypothetisches 35er mit Nahgrenze 0,30m (Beta[Ng]=0,15):

Beta[25mm] = (0,15*35mm + 25mm)/35mm = 0,86

[Jens N.]

Zitat von bleibert

Na, einfach ausrechnen!

"Einfach" ist gut Ich versuche da mal durchzusteigen, vielen Dank.

[bleibert]

Zitat von Jens N.

"Einfach" ist gut Ich versuche da mal durchzusteigen, vielen Dank.

Na, zum Glück habe ich gerade ein Blatt, einen Stift und einen Scanner hier rumliegen. Mit der Skizze und der handschriftlichen Notierung wird's vielleicht einfacher. Es sind nur zwei optische Grundformeln, die zum Einsatz kommen.

[RainerV]

Kleiner Tipfehler in der ersten Formel:
1/f=1/b+1/g

Meines Wissens weicht die Brennweite bei der Naheinstellgrenze vielfach erheblich von der Brennweite bei Unendlich ab. Ich dachte, ich hätte die Brennweite bei der Naheinstellgrenze früher in der bekannten Objektivübersicht bei Michael Hohner gelesen, finde sie aber nicht mehr. Ist also Einbildung oder die Tabelle ist verändert worden.

Und mit den Infos aus der Tabelle von Michael Hohner müßte man dann wohl anders umformen. Habe mir das jetzt zugegebenerweise nicht genauer angeschaut.

Rainer

[bleibert]

Zitat von RainerV

Kleiner Tipfehler in der ersten Formel:
1/f=1/b+1/g

Oh ja, vielen Dank. Ich hab's gleich korrigiert.

Meines Wissens weicht die Brennweite bei der Naheinstellgrenze vielfach erheblich von der Brennweite bei Unendlich ab.

Das gilt nur für Objektive mit einer der vielen Arten von Innenfokussierung. Das sind zB alle Zoomobjektive (einzige mir bekannte Ausnahme ist das MC/MD Zoom Rokkor 1:2,8 40-80mm, das ist tatsächlich auszugsfokussiert). Festbrennweiten sind i.d.R auszugsfokussiert, d.h. das gesamte Linsenpaket wandert bei der Fokussierung hin und her. Bei AF-Objektiven kommt allerdings öfter auch mal eine Innenfokussierung vor, insbesondere bei längerbrennweitigen Objektiven. Bei der Innenfokussierung werden nur bestimmte Objektivgruppen im Inneren verschoben, oder auch die Frontgruppe oder Rückgruppe. Somit müssen kleinere Massen bewegt werden, und das macht den AF schneller. Dabei wird im Extremfall die Brennweite deutlich verkürzt:

Nehmen wir zB ein Objektiv mit 300mm Brennweite. Bei Fokussierung auf Unendlich beträgt die Bildweite 300mm, ist also gleich der Brennweite. Verkürzen wir jetzt die Brennweite auf 270mm - was ja in der Bildwirkung kaum auffallen dürfte - , behalten aber die Bildweite bei (also 300mm), ergibt sich jetzt folgende Gegenstandsweite:

g = (b*f)/(b-f) = (300mm * 270mm)/(300mm - 270mm) = 2700mm = 2,7m

Somit ergibt eine kaum sichtbare Änderung der Brennweite schon eine sehr nahe Fokussierung.

[Jens N.]

Zitat von RainerV

Ich dachte, ich hätte die Brennweite bei der Naheinstellgrenze früher in der bekannten Objektivübersicht bei Michael Hohner gelesen, finde sie aber nicht mehr. Ist also Einbildung oder die Tabelle ist verändert worden.

Ist keine Einbildung, Mhohner hat diese Angabe wohl entfernt, leider.

@Dennis: vielen Dank für die Mühe, auch wenn ich's leider auf Anhieb nicht durchschaue. In einer ruhigen Minute versuche ich es mal auf den Schirm zu kriegen, jetzt beschäftigt mich erstmal ein neues Spielzeug (Sony DSC-V3).

[bleibert]

Noch was zur Nahgrenze: Die kannst Du leider nicht so ohne weiteres einfließen lassen. Die obige Betrachtungsweise ist eine stark vereinfachte, und gilt für sogenannte "dünne" Linsen, bei denen es nur eine Hauptebene gibt. Ein Objektiv ist aber eine Konstruktion aus mehreren Linsen, eine "dicke" Linse. Das schlägt sich im Modell so nieder, dass man die Hauptebene in eine vordere (gegenstandsseitige) und eine hintere (bildseitige) aufteilt, und den Raum dazwischen gewissermaßen als "Blackbox" betrachtet, der nicht in die Berechnungen mit eingeht, so dass man wieder mit obigen Formeln rechnen kann. Die Nahgrenze beschreibt allerdings (wie alle Markierungen auf dem Fokusring) den Abstand zwischen Gegenstand und Bild. Und dabei spielt der Abstand der Hauptebenen eine Rolle:

Nahgrenze = Bildweite b + Abstand der Hauptebenen h + Gegenstandsweite g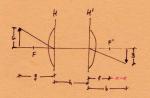



Den Abstand der Hauptebenen kannst Du so ermitteln:

Sei bei obigem hypothetischem 135er die Nahgrenze ng=1m=1000mm und der dabei erzielte Abbildungsmaßstab Beta[ng]1:5=0,2. Somit lassen sich Bildweite und Gegenstandsweite berechnen:

b = Beta*f + f ........ (wie oben hergeleitet)

b[ng] = 0,2*135mm + 135mm = 27mm + 135mm = 162mm

1/f = 1/g + 1/b

1/g = 1/f - 1/b = (b-f)/(b*f)

g = (b*f)/(b-f)

g[ng] = (162mm * 135mm)/(162mm - 135mm) = 810mm

ng = b + h + g

h = ng - b - g = 1000mm - 162mm - 810mm = 28mm

Dieser Hauptebenenabstand bleibt immer gleich, somit kannst du jetzt damit auch für andere Entfernungen Berechnungen anstellen.